1. 데이터 전처리
* 데이터 정제 과정
- 수집 : 다양한 매체로부터 데이터 수집
- 저장 : 원하는 장소에 저장
- 변환 : 원하는 형태로 변환
- 품질확인 : 활용가능성을 타진하기 위한 품질확인
- 관리 : 사용이 원활하도록 관리
* 데이터 전처리의 주요 작업
- 정제 : 결측 데이터, 이상치 파악 및 제거, 정합성 맞도록 교정하는 작업
- 통합 : 여러 개의 데이터 베이스, 데이터 집합 또는 파일을 통합하는 작업
- 축소 : 샘플링, 차원축소, 변수 선택 및 추출을 통해 차원을 줄이는 작업
- 변환 : 데이터를 정규화, 이상화, 파생변수 등으로 변환하는 작업
* 데이터 정제 작업
- 결측값 : 대체(중위수, 평균 등)
- 노이즈 : 데이터 평활화 기법 사용. 구간화, 회귀, 군집화
- 아웃라이어 : 기준선으로 대체(상한 초과면 상한, 하한 미만이면 하한값으로)
* 결측치 유형
- 완전 무작위 결측(MCAR) : 결측치가 다른 변수와 아무런 상관이 없는 경우. 일반적인 결측치
+ 고의성 없이 응답을 빠트린 경우. 보통 제거하거나 단순 무작위 표본추출을 통해 보완
- 무작위 결측(MAR) : 결측값이 결측된 변수와 관련이 없지만 다른 변수들과 관련이 있는 경우, 결측이 완전히
설명될 수 있음
+ 예를들어 여성이 남성보다 체중을 기입하지 않는다라고 하면 체중에 결측값이 생기지만 체중변수와 관련이
있는 것이 아닌 성별 변수와 관련이 있는 것임
- 비 무작위 결측(NMAR) : 위 두가지가 아닌 경우. 결측값이 결측된 변수와 관련이 있는 경우
+ 서비스에 불만족한 고객은 만족도 설문에 응답하지 않음
* 결측치 대치법
- 단순 대치법 : 결측치를 ‘완전 무작위 결측’ 또는 ‘무작위 결측’으로 판단하고 처리
+ 완전분석법 : 불완전한 자료 무시, 완전하게 관측된 자료만 분석. 통계적 추론의 타당성문제 발생 위험
+ 평균대치법 : 평균값으로 결측치를 대치. 통계량의 표준오차가 과소 추정될 수 있음. 비조건부 평균대치법
+ 회귀대치법 : 회귀분석 예측치로 결측치 대체. 조건부 평균대치법
+ 단순확률대치법 : 평균대치법에서 표준오차 과소추정문제 보완법. 확률추출에 의해 전체 데이터 중 무작위로
대치하는 방법(핫덱법)
+ 최근접대치법 : 전체표본을 몇 개의 대체군으로 분류, 각 층에서 응답자료를 순서대로 정리 후 결측값 바로
이전 응답을 결측치에 대치. 응답이 여러번 사용되는 문제 발생
- 다중 대치법 : 단순 대치법을 복수로 시행, 통계적 효율성 및 일치성 문제를 보완
+ n개의 단순대치를 통해 n개의 새로운 자료를 만들어 분석을 시행, 얻어진 통계량 및 분산결합을 통해 통합
* 이상치
- 이상치(outlier) : 정상의 범주(데이터의 전체적 패턴)에서 벗어난 값
- 이상치가 비무작위로 나타나면 데이터의 정상성 감소를 초래하고 이는 신뢰성 저하로 연결
- 이상값이 오류가 아닐 수 있음. 도메인 전문가와 상의 후 처리
- 오류일 경우 제거하거나 무시하고, 특이값인 경우 특이사항 고려하여 분석
* 모수
① 모수(parameter) : 모집단(전체 집단)의 모평균, 모표준편차, 모분산 등
② 모수적 방법 : 정규분포를 따른다는 가정으로 모수적 특성을 이용하는 통계적 방법
③ 비모수적 방법 : 정규분포임을 가정할 수 없을 때 사용하는 방법
* 이상값 탐지 방법
① 단변량 자료에서의 탐지 : 사전에 정의된 이상치 영역에 포함여부
- 시각화 방법 : 박스 플롯, 산점도
- 표준화 점수(Z값)
- 통계적 가설검정
- 카이제곱 검정(교차분석)
② 다변량 자료에서의 탐지 : 연관성이 존재하는 2개 이상의 변수 정보 활용, 거리, 밀도 등을 활용하여 파악
- 회귀진단 : 레버리지, 표준화잔차 등
- 군집분석시 마할라노비스 거리
- LOF(Local Outlier Filter) : 밀도기준
- 의사결정나무
* 이상값 처리 방법
① 관측치 삭제 : 오류 및 이상관측치가 매우 작다면 삭제
② 변환과 범주화 : 자연로그 활용(극단값 축소), 결정트리(변수의 구간화)
③ 대치 : 결측치 대치와 동일한 방법.
2. 변수
* 변수선택 방법
― 변수는 기본적으로 많을수록 신뢰성이 높아지나 더 작은 변수를 사용 시 동일한 설명력이 나온다면 효율성이 증가
― 예측 정확도 측면에서 가장 좋은 성능을 보이는 Feature Set을 뽑아내는 방법
― 여러번 기계학습을 진행하기 때문에 시간과 비용이 높지만 최종적으로 Best Feature Set을 뽑을 수 있음
① 전진 선택법(Forward Selection)
+ 변수가 없는 상태로 시작
+ 종속변수와 단순상관계수의 절댓값이 가장 큰 변수를 분석모형에 포함시키는 것
+ 가장 좋은 변수를 추가하여 성능 향상이 없을 때까지 반복
+ 한번 추가한 변수는 제거하지 않음. 부분 F검정
② 후진 소거법, 후진선택법, 후진제거법(Backward Selection Elimination)
+ 모든 변수를 가지고 시작
+ 종속변수와 단순상관계수의 절댓값이 가장 작은 변수를 분석모형에서 제외시키는 것,
+ 가장 덜 중요한 변수를 제거하며 모델 향상
+ 제거한 변수는 추가하지 않음
③ 단계적 선택법
+ 전진 선택법을 통해 가장 유의한 변수를 모형에 포함
+ 나머지 변수들에 대해 후진 선택법을 적용하여 새롭게 유의하지 않은 변수들 제거
+ 제거된 변수는 다시 추가하지 않고 설명변수가 없을 때 까지 반복
* 차원 축소의 필요성(차원이 클 경우 문제점)
① 자원이 많이 필요 : 컴퓨팅 파워 필요, 비효율적
② 과적합 문제 발생
③ 설명력 저하 : 내부구조 이해가 어렵고 해석이 어려워짐
④ 차원의 저주 : 차원이 증가하면 학습데이터의 수가 차원의 수보다 적어져 성능이 저하되는 현상
- 차원을 줄이거나 데이터의 수를 늘려야 함
* 차원축소의 방법
① 다차원척도법(MDS) : 거리를 기준으로 차원수를 줄여서 대개 2차원 공간에 표시하는 방법
② 주성분분석(PCA) : 분포된 데이터들의 특성을 설명 할 수 있는 하나 또는 복수 개의 특징을 찾는 것
+ 서로 연관성이 있는 고차원공간의 데이터를 선형연관성이 있는 저차원(주성분)으로 변환하는 과정을 거침
(직교변환)
+ 다수의 변수를 축약하여 소수로 줄이는 역할
+ 기존의 기본변수들을 새로운 변수의 세트로 변환하여 차원을 줄이되 기존 변수들의 분포특성을 최대한
보존하여 이를 통한 분석결과의 신뢰성을 확보
+ 음식점 만족도 설문시 대기시간, 청결도, 음식맛, 신선도 조사시, 대기시간과 청결은 ‘서비스’, 음식맛과
신선도는 ‘음식의 질’ 이라는 요인으로 해석
+ 특징
→ 차원 축소에 폭넓게 사용됨. 어떠한 사전적 분포 가정의 요구가 없음
→가장 큰 분산의 방향들이 주요 중심 관심으로 가정
→ 본래의 변수들의 선형결합으로만 고려
→ 차원의 축소는 본래의 변수들이 서로 상관이 있을때만 가능
→ 스케일에 대한 영향이 크다. 즉, PCA 수행을 위해선 변수들 간의 스케일링이 필수
③ 요인분석(Factor Analysis) : 변수간 상관관계를 분석하여 공통차원을 축약하는 통계분석
+ 독립변수/종속변수 개념이 없음, 주로 기술통계 방법 활용
+ 관련된 변수들을 군집화 함으로 요인간의 상호 독립성 및 변수의 특성을 파악
+ 아이겐값으로 추출요인수 결정
+ 커뮤낼리티(설명되는 정도)
* 요인분석의 목적
- 변수축소 : 여러 개의 관련 변수가 하나의 요인으로 묶임
- 변수제거 : 요인에 포함되지 않거나 중요도가 낮은 변수 제거
- 변수특성파악 : 관련된 변수들의 묶음으로 상호 독립특성을 파악하기에 용이
- 측정항목 타당성 평가 : 그룹이 되지 않은 변수의 특성을 구분할 수 있게 됨
- 요인점수를 활용한 변수 생성 : 회귀분석, 군집분석, 판별분석 등에 활용 가능한 변수 생성
④ 특이값 분해(SVD) : 적당한 특이값을 이용해 원래 데이터와 비슷한 정보력을 가지는 차원을 만들어 냄
+ 비 정방행렬에 적용 가능
+ 데이터 축소, 영상처리 및 압축, 이상치 감지 등에 활용
⑤ 선형판별분석(LDA) : 사전에 집단이 나누어져 있음
+ 집단 내 분산 대비 집단간 분산 차이를 최대화 하는 독립변수의 계수를 찾는 과정
⑥ 음수 미포함 행렬분해 : 음수를 포함하지 않은 행렬 V를 행렬 W와 H의 곱으로 분해, 행렬 곱셈에서
V보다 W, H가 적은 차원을 가짐. 정확한 해가 없으므로 대략적 해를 구함
* 파생변수
- 기존의 변수를 조합하여 새로운 변수를 만들어 내는 것
- 사용자가 특정 조건을 만족하거나 특정 함수에 의해 값을 만들어 의미를 부여하는 변수로 매우 주관적일 수
있으므로 논리적 타당성을 갖출 필요가 있음
- 고객관리 등에 유용하게 사용됨
* 요약변수
- 수집된 정보를 분석에 맞게 종합한 변수
- 데이터마트에서 가장 기본적인 변수
- 많은 분석 모델에서 공통으로 사용될 수 있어 재활용성이 높음
* 변수변환
① 데이터를 분석하기 좋은 형태로 바꾸는 작업, 어떤 변수로 나타낸 식을 다른 변수로 바꿔 나타냄
② 데이터 전처리 과정 중 하나로 간주
③ 범주형 변환, 정규화(일반, 최소-최대, Z-Score), 로그 변환, 역수 변환. 지수 변환, 제곱근 변환 등
* 정규변환
― 변수변환을 통해 정규분포를 따르도록 하는 것
① 로그변환 : 정규성을 높이는 방법. 데이터 간 편차를 줄여 왜도와 첨도를 줄일 수 있음.
+ 데이터가 좌측으로 치우친 경우 정규분포화를 위해 로그 변환
+ 로그를 취하면 그 분포가 정규분포에 가깝에 분포하는 경우가 있음. 이를 로그정규분포를 가진다고 함
+ 주식가격의 변동성 분석 등
② 제곱근변환 : 좌측으로 약간 치우친 경우 사용. 제곱근을 사용하면 선형적인 특성을 가지게 됨
③ 지수변환 : 데이터가 우측으로 치우친 경우 사용
④ 박스-콕스 변환 : 데이터 분산을 안정화 하는 역할
* 분포형태별 정규분포변환

* 범주형 변환
― factor
① 구간화 : 소득분위, 연령층 등
② 더미변수 : 더미분석
③ 데이터 인코딩 : 범주형 데이터를 숫자형으로 바꾸는 것
* 정규화
① 최소-최대 정규화 : 모든 feature를 최소값 0, 최대값을 1로 변환하는 것
+ (x-최소값) / (최대값-최소값)
+ 아웃라이어의 영향이 클 수 있음
② Z-score 표준화

* 클래스 불균형
- 각 클래스가 갖고 있는 데이터의 양에 차이가 큰 경우
- 불균형 상태에서 분석시 정확도가 높아도 데이터가 적은 클래스의 재현률이 떨어질 수 있음
- 클래스 균형은 소수의 클래스에 특별히 더 큰 관심이 있는 경우 필요함
* 가중치 균형방법
― 데이터 loss 계산시 특정 클래스 데이터에 더 큰 loss값을 갖도록 하는 방법
① 고정비율 이용 : 클래스 비율이 1:5인 경우 가중치를 5:1로 주어 균형을 맞추는 방법
② 최적비율 이용 : 도메인 특성과 최종성능을 고려해 가중치 비율의 최적 세팅을 찾아가는 방법
* 데이터 샘플링 방법
― 다수 클래스와 소수 클래스의 샘플개수를 조정하여 정밀도를 향상시켜 데이터 집합을 구성하는 방법
① 언더 샘플링 : 대표클래스의 일부만 선택하고 소수클래스는 최대한 많은 데이터 사용
- 대표성이 있어야 함. 정보손실 문제가 있음
② 오버 샘플링 : 소수클래스의 복사본을 만들어 대표클래스 수 만큼 데이터를 만들어 주는 것.
- 똑같은 데이터를 복사하는 것이므로 새로운 데이터는 기존 데이터와 같은 성질을 갖게 됨
3. 데이터 탐색
* 탐색적 자료분석(EDA)의 주요 확인사항
① 분석의 목적, 변수, 개별변수의 이름, 설명 확인
② 데이터 문제성 확인 : 데이터 결측치 유무, 이상치 유무 확인. head, tail 확인
③ 데이터 분포상의 이상형태 확인(데이터 개별 속성값이 예상한 범위 분포를 가지는지 확인)
④ 데이터간 관계 확인(상관도를 산점도 등을 통해 확인)
* 분석의 종류
- 진단분석 : 원인이 무엇인가?
- 기술분석 : 무엇이 일어났는가?
- 예측분석 : 어떻게 될 것인가?
- 처방분석 : 어떻게 해야 할 것인가?
* 상관분석 기본가정
- 선형성 : 두 변인 X와 Y의 관계가 직선적인지 알아보는 것
- 동변량성 : X값에 관계없이 Y의 흩어진 정도가 같은 것 ↔ 이분산성
- 정규분포성 : 두 변인의 측정치 분포가 모집단에서 모두 정규분포를 이루는 것
- 무선독립표본 : 모집단에서 표본을 뽑을 때 표본 대상이 확률적으로 선정되는 것
* 공분산
① 2개의 변수값을 갖는 개별 관측치들이 각 변수의 평균으로부터 떨어진 정도를 나타내는 지표
②각 변수의 측정단위가 달라지면 공분산의 관계성 파악이 어려움. 표준화 필요(상관계수)
* 피어슨 상관계수
- 수치적 데이터 변수간의 상관분석. 일반적으로 진행하는 상관분석(등간, 비율척도)
- +1 과 -1 사이의 값, +1은 완벽한 양의 선형 상관관계, 0은 선형 상관관계 없음, -1은 완벽한 음의 선형 상관관계
* 스피어만 상관계수
- 이산형, 순서형 데이터 변수간 상관분석 또는 두 연속형 변수가 정규분포를 심하게 벗어난 경우
- 비선형 관계의 연관성 파악 가능
* 중심화 경향

* 산포도

* 기타
① 평균 절대 편차 : 관측값에서 평균을 빼고, 절댓값을 취하여 산술평균
② 사분위범위 : 자료를 크기 순으로 배열 후 3사분위수(Q3) – 1사분위수(Q1)로 정의
③ 왜도 : 분포가 어느 한쪽으로 치우친 정도를 나타내는 통계적 척도
+ 오른쪽 꼬리 : 왜도>0, 최빈값 < 중앙값 < 평균
+ 왼쪽 꼬리 : 왜도<0, 평균 < 중앙값 < 최빈값
+ 피어슨의 비대칭계수(CS) : 3*(평균-최빈값)/표준편차 또는 3*(평균-중앙값)/표준편차
→ CS=0 정규분포, CS>0 오른쪽 꼬리, CS<0 왼쪽 꼬리
④ 첨도 : 중심에 집중여부, 분포의 뾰족한 정도
+ 첨도 = 3 : 표준정규분포와 중첩
+ 첨도 > 3 : 표준정규분포보다 정점이 높고 뾰족한 모양
+ 첨도 < 3 : 표준정규분포보다 낮고 납작한 모양
⑤ 상자수염그림(Box Plot) : 수치적 자료 표현, 자료로부터 얻어 낸 통계량(최솟값, Q1, Q2, Q3, 최댓값)을
가지고 그림, 이상치는 파악 가능하나 분산과 같은 퍼짐정도는 파악 어려움
* 시각적 데이터 탐색
① 히스토그램 : 도수분포표를 표로 나타낸 그림
② 줄기-잎 그림 : EX) 줄기 10자리, 잎은 1자리 표시. 자료구조 파악 쉬움. 통계표와 차트의 중간형태
|
줄기
|
잎
|
|
3
|
2, 3, 3, 4, 5, 7, 9
|
|
4
|
0, 0, 1, 2, 5, 8, 8, 9, 9, 9
|
|
5
|
4, 5, 6, 7, 7
|
|
6
|
3, 8, 9
|
③ 막대그래프, 파이차트, 산점도
④박스플롯
* 시간, 공간 데이터
- 시간 데이터 : 데이터에 유효 시간, 거래 시간, 사용자 정의 시간과 같은 연관된 시간 표현 정의
- 공간 데이터
+ 비공간 타입 : 기본적인 데이터 유형을 가진 속성
+ 래스터 타입 : 실세계에 존재하는 객체의 이미지
+ 벡터 타입 : 점. 선. 면 등의 요소로 구성
+ 기하학적 타입 : 벡터 타입의 요소로부터 거리, 면적, 길이 등과 같은 유클리드 기하학 계산값으로 표현
+ 위상적 타입 : 공간 객체간의 관계 표현. 방위, 공간 객체간의 중첩, 포함, 교차, 분리 등. 동적으로 계산
* 시공간자료 질의어
① 시공간자료 정의언어
- 시공간 테이블 인덱스 및 뷰의 정의문, 변경문 등
- 공간적 시간적 속성을 동시 포함
② 시공간자료 조작언어
- 객체의 삽입, 삭제, 변경 등의 검색문
- 시간지원, 공간 연산자를 포함, 공간관리와 이력정보 제공
4. 분포
* 데이터 요약
① 모수통계 : 등간/비율척도. 모집단의 특성(분포, 표본오차 등) 정보가 충분. 표본통계량으로 모수추정 가능
② 비모수통계 : 명목/서열척도. 모집단의 분포나 모수의 특징을 추론하기 어려운 경우 사용하는 기법
* 확률 표본 추출 기법
① 단순무작위 추출 : 가장 기본이 되는 표본추출
② 계통(체계적) 추출 : 모집단에서 추출간격을 설정하여 간격 사이에서 무작위 추출, K번째
③ 층화 추출 : 모집단이 이질적 몇 개 층으로 구분할 수 있는 경우. 내부동질 외부이질. 계층별 무작위
- 최적 배분법 : 추정량의 분산을 최소화 시키거나 주어진 분산의 범위 하에서 비용을 최소화 시키는 방법
- 비례 배분법 : 각 층 내의 추출단위 수에 비례하여 표본크기를 배분하는 방법
- 네이만 배분법 : 각 층의 크기와 층별 변동의 정도를 동시에 고려한 표본배정 방법
④ 군집 추출 : 동질적인 소그룹으로 나눌 수 있는 경우. 일부 그룹에서 표본추출
* 표본추출 오차
- 표본에서 선택된 대상이 모집단의 특성을 추정함으로써 발생하는 모집단과 표본의 오차 범위
- 과잉 대표 : 중복선택 등의 원인으로 모집단이 반복·중복된 데이터만으로 규정되는 현상
- 최소 대표 : 실제 모집단의 대표성을 나타낼 표본이 아닌 다른 데이터가 표본이 되는 현상
- 표본추출시 표본의 크기보다 대표성을 가지는 표본을 추출하는 것이 중요
5. 확률분포
* 조건부 확률

* 결합 확률
- 사건 A와 B가 동시에 발생하는 확률
- 확률의 곱셈 법칙 𝑃(𝐴)×𝑃(𝐵)=𝑃(𝐴∩𝐵)
- 배반사건 : 두 확률A, B가 동시에 일어날 수 없을 때 A, B는 서로 배반하였다고 한다. 𝐴∩𝐵=Φ
* 베이지안 정리
- 어떤 사건이 발생했다는 조건 하에서 다른 사건이 발생할 확률을 계산하는데 사용

- 사건 B가 발생했다는 것이 주어진 상황에서 사건 A가 발생할 확률인 P(A|B)를 계산할 수 있음
* 확률변수와 확률분포
① 확률변수 : 사건 시행의 결과(확률)를 하나의 수치로 대응시킬 때의 값, 확률값
- 이산확률변수 : 확률변수가 취할 수 있는 값이 유한. 동전 앞뒤 확률 등
- 연속확률변수 : 무한변수. 확률이 범위로 나타남
② 확률분포 : 수치로 대응된 확률변수의 개별 값들이 가지는 확률값의 분포, 확률변수가 취할 수 있는 값의 수가
유한하면 이산확률분포, 무한하면 연속확률분포
* 이산확률분포


* 연속확률분포


* 용어정리
① 자유도 : 자료집단의 변수 중에서 자유롭게 선택될 수 있는 변수의 수
② 표본분포 : 크기 n의 확률표본(모집단에서 동등한 확률로 추출된 개체들의 집합)의 확률변수의 분포
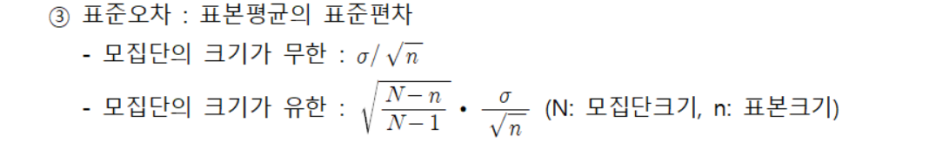
④ 중심극한정리 : 모집단의 분포에 상관없이 표본의 수가 큰 표본분포들의 표본평균의 분포는 정규분포를 이룸
⑤ 표본비율 : 표본을 구성하는 n개의 개체 중에서 성공으로 나타나는 개체 수의 비율
* 표본분포


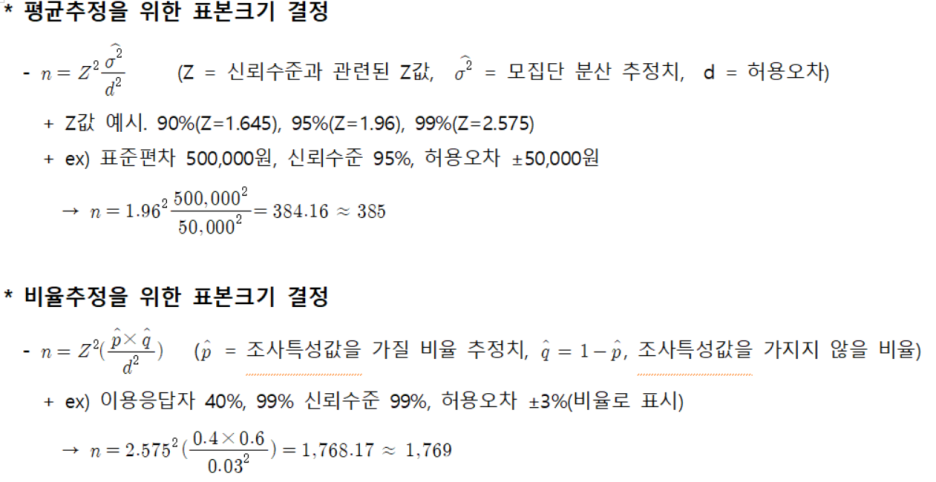
* 중심극한정리
① 동일한 확률분포를 가진 독립확률변수 n개의 평균의 분포는 n이 적당히 크면 정규분포에 근사함
6. 통계적 추론
* 통계적 추론의 종류
① 점추정 : 모수를 단일치로 추측, 신뢰도를 구할 수 없는 단점
② 구간추정 : 모수를 포함한다고 추측되는 구간을 구하는 방법. 신뢰도를 함께 구할 수 있음
* 추정량의 선택기준
① 불편추정량 : 모든 가능한 추정치의 평균이 모수의 참값과 같아야 함
- 표본평균은 불편추정량. 표본분산은 불편추정량이 아님
② 효율성 : 불편추정량 중 그 분산이 작은 추정량
③ 일치성 : 표본크기가 증가할수록 좋은 추정값 제시
④ 충분성 : 동일한 크기 표본으로부터 가장 많은 정보를 제공하는 추정량

* 편향
- 기대하는 추정량과 모수의 차이, 편향이 0이 되면 불편추정량


* 신뢰도(신뢰수준)와 신뢰계수
① 신뢰도 : 1시그마(68.27%), 2시그마(95.45%), 3시그마(99.73%)
② 신뢰계수(Za/2) : 0.9(1.645), 0.95(1.96), 0.99(2.57)
③ 표본크기 결정요인
- 신뢰도 : 표본의 크기가 클수록 신뢰도가 높아짐
- 표준편차 : 표준편차가 클수록 표본이 커야 함
- 오차의 크기 : 오차를 작게 하려면 표본이 커야 함
* 가설검정
① 가설검정 : 검정통계량의 표본분포에 따라 채택여부를 결정짓는 통계적 분석과정
② 귀무가설(H0) : 현재 통념적으로 믿어지고 있는 모수에 대한 주장 또는 원래의 기준이 되는 가설
③ 대립가설(H1) : 연구자가 모수에 대해 새로운 통계적 입증을 이루어 내고자 하는 가설
* 가설검정의 순서
|
① 가설의 설정
② 유의수준 a의 결정 |
|
|
i) 검정통계량을 사용할 때
|
ii) p값을 사용할 때
|
|
③ 유의수준 a에 해당하는 임계치 및 기각영역의 결정
④ 검정통계량의 계산 ⑤ 의사결정 |
③ 검정통계량의 계산
④ p값의 계산 ⑤ 의사결정 |
* 검정의 오류
① 1종오류 : 귀무가설이 참이여서 채택해야 함에도 거부하는 경우
② 2종오류 : 귀무가설이 허위라서 거부해야 함에도 채택하는 오류
|
|
H0가 참
|
H0가 거짓
|
|
H0 채택
|
옳은 결정
(신뢰수준)=1-a |
2종오류
확률=b |
|
H0 기각
|
1종오류
확률=a |
옳은 결정
(신뢰수준)=1-b |
* 주요용어
① 유의수준 : 귀무가설이 맞는데 틀렸다 결론 내리게 될 확률, 제1종 오류를 범할 확률의 최대 허용한계
② p-value : 귀무가설을 기각하려고 할 때 필요한 최소의 유의수준


'단비 블로그 > 배움의 단비 (공부)' 카테고리의 다른 글
| [빅데이터분석기사] 4. 결과해석 (0) | 2024.05.30 |
|---|---|
| [빅데이터분석기사] 3. 모델링 (0) | 2024.05.30 |
| [빅데이터분석기사] 1. 빅데이터 분석기획 (0) | 2024.05.30 |
| 케글연습 첫날 (22.08.23) (0) | 2024.05.30 |
| [원가관리회계] II. 제품원가계산(원가회계) #.1 (0) | 2024.05.30 |



